Excel Maniacs

関数で出来ますか～？（第５問解答例）

　お題はスロットマシーン。問題はこちら。

解答はいろいろ、あると思います。

まずは一番オーソドックスなやつ。

=AND(D4=F4,F4=H4)　17文字

これが基本ですね。

ちょっと気取って・・・

=COUNTIF(D3:H3,D3)=COUNTA(D3:H3)　32文字

これは右辺を弄れば・・・

=COUNTIF(D3:H3,D3)=3　　　20文字

最後に相加平均≧相乗平均の関係で・・・

*

*

*

*

等号の成立する場合はx=y=zの場合でしたね・・・

=AVERAGE(CODE(D3),CODE(F3),CODE(H3))=GEOMEAN(CODE(D3),CODE(F3),CODE(H3))

12文字のやつは一番先に言ったminmaxさんにお任せします。

関数で出来ますか～？（第５問）

　お題は「スロットマシーン」です。

F９キー（三四郎はShiftを押しながらF2）を押すと下図のような３種のマークが切り替わります。

当たりならばセルJ3に「TRUE」と、ハズレならば「FALSE」と

表示させて下さい。

*

*

*

*

*

※解答用参考ブック

Slot_Q5.xlsをダウンロード （エクセル版）

Slot_Q5.jsdをダウンロード （三四郎版）

※今回のルール（と言いましょうか・・・）

この問題はエクセルコンテストで言えば「腕自慢」ではなくて

「腕試し」というべきものです。今まで何らかの形でこのブログに参加して

頂いた方、特に常連さんはその辺りをご配慮下さい。m(__)m

尚、答え合わせは2/18（水）の7:00ということで・・・

関数で解けますか？ （ランダム得点入力解答例 その4）

【´･ω･`】:さて、どん尻に控えしは～！！ 誰あろう、minmaxさ～ん！！

****************************************************************************************

仕事の飲み会から帰ってきて・・・
無線を止めてルーター直結で無理矢理つなげたらとりあえずつ
ながりました。
みなさんのはよく見てませんが、
次はつながるか分からないのでつまらないずるですが思い切っ
て送ります。

以下は、昨日送ろうとしたときに書いたものです。
－－－－－－－－－－－－－－－
くまぷーさんお世話になっております。
今回は、参加しないと心に決めていたのですが、
みなさんが頑張っておられるので、ちょっとやってみました。
何の工夫も飾り気もありませんが、一応送ります。

２日ぶりにパソコンを開いてエクセルをさわっていたら、
ネットワークにつながらなくなり、
２度もブルースクリーンになってしまいました。
起動に５分以上かかるし、超遅いし、
このパソコンも寿命のようです。
それともウイルスかな。
エクセルの方は殴り書きの検証不足のものですのがよろしくお
願いします。
念のためウイルスチェックはよろしくお願いします。

minmax_san_2009_Q5.zipをダウンロード

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（minmaxさん談）

***********************************************************************************

>念のためウイルスチェックはよろしくお願いします。

一応、ソースネクストのやつでチェックしました。

陰性でした。（念のため）　(^^ゞ

関数で解けますか？ （ランダム得点入力解答例 その３）

★MFさん

くまぷー　さん

お世話になっています。

修正出来ましたので、差し替えお願いします。
ファイル名は同じにしてあります。

よろしくお願いします

mf_2009_Q5.lzhをダウンロード
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ＭＦさん談）

****************************************************************************

★sakudaさん、循環参照版

時間切れで大した物は思いつきませんでした。

循環参照バージョンです。
sakuda89.lzhをダウンロード

****************************************************************************

★くまぷー、循環参照版

sakudaさんに刺激されて作ってみました。(^^ゞ

2009_Q5_kumapooh_Jyunkan01.lzhをダウンロード

*****************************************************************************

★かめぷーさん

ちょっと過ぎちゃったぁ！
ごめんなさい！
とりあえず送ります。

kamepooh_san_2009_Q5.lzhをダウンロード

関数で解けますか？ （ランダム得点入力解答例 その２）

★かずさん

こんばんは、くまぷーさん。

ここんとこちょっと忙しくて…
それに、最近思考回路がすっかり旧式になってしまって…

とりあえず、関数での参加をお願いします。
要求される回答にはなっているとは思います。

まだ締め切りには間に合いますよね。

では、よろしくお願いします。

KazuSan_2009_Q5.lzhをダウンロード

                    （かずさん談）

**********************************************************************************

★ジョー３さん

親切にと思って、操作の所に色を付けたら

・・・・・

ズル版に影響が出るのだ。

先頭がタイトルと理解されて

Aｚでは、うまく行かないのだった。

まあ、皆さんは分かって下さると思うが、、、

説明が　作品に影響　そんなことはあるよねーー

J3San_2009_Q5.zipをダウンロード

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ジョー３さん談）

**********************************************************************************

★kirさん

くまぷーさん　こんばんわ。ご無沙汰してました。

いまさらながらですが、Ｑ４のminmaxさんの式を参考にしたものと、Ｑ５を２ファイル送ります。
「2009_Q5-2」はオプション弄ってますのでファイルを分けました。よろしくお願いします。

kir_san_2009_Q5.lzhをダウンロード

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（kirさん談）

関数で解けますか？ （ランダム得点入力解答例 その１）

★くまぷー

　入力は出席番号２桁+得点としています。

　例）出席番号１番+63点→0163

　　　出席番号20番+63点→2063

　　　出席番号20番+1点→201

　　　出席番号20番+100点→20100

つまり、上2桁が出席番号を示し、残りが得点を示しています。

こうすることにより、ユーザは最小のストロークで成績処理を

行うことが出来ます。

　・関数版

　　=--MID(VLOOKUP(B2 & "*",A$2:A$46,1,0),3,9)　　42文字

　　エラーを隠して

　　=IFERROR(--MID(VLOOKUP(B2 & "*",A$2:A$46,1,0),3,9),"")　54文字

2009_Q5_kumapooh_Func.lzhをダウンロード

　・マクロ版

　ワークシートのチェンジイベントを使うことで1行マクロにしました。

　尚、文字数を稼ぐためにデフォルトの引き数名を弄っています。

Private Sub Worksheet_Change(ByVal T As Range)
       'On Error Resume Next  '有効にすればデータを消去したさいの
                               'エラーを回避（無視）できます。(^^ゞ
       If T.Column > 2 Then Cells(Left(T, 2) + 1, 2) = Mid(T, 3)
End Sub

2009_Q5_kumaPooh_Macro.xlsをダウンロード

**********************************************************************************

★y sakudaさん

　1行マクロ2作、配列数式1作の計3作です。

　sakuda_san_2009_Q6.lzhをダウンロード

**********************************************************************************

★む印さん

少しだけコンテスト風にアレンジしてみましたｄ
よろしくお願いしま～す！

2009_Q5_Mujirushi_san.lzhをダウンロード

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（む印さん　談）

関数で解けますか？(その2)

　前回の「10枚の領収書」は如何だったでしょうか？

今回のお題は「ランダム得点入力」です。(^O^)

このブログは「教員のためのPC活用術」というタイトルなのですが

この頃はぜんぜん教員を意識した記事がありません。たまには・・・

ということで上記のお題にしてみました。

　さて、業界人（教員）以外の方にお題の背景を説明しますと・・・

この業界では中間試験・期末試験からちょっとした小テストまで

年がら年中試験をやっています。中間試験・期末試験等の定期試験では

生徒が出席番号順に着席しています。ですから答案回収時に答案が出席番号順に

なるので、採点結果を名簿に記入（入力）する時に不便はないのですが

定期試験以外の小テスト等になると、生徒が出席番号順に着席していないので

回収した答案は当然、バラバラです。

　このような答案の採点結果を記入（入力）する時は視線を動かし

入力するセルを探し、そのセルにカーソルを移動し入力しなければ

ならないので、たいへん面倒です。(T.T)

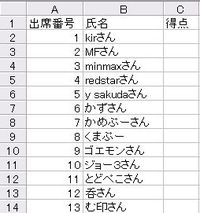
★名簿は下のようになっています。

*

*

*

*

*

*

*

*

*

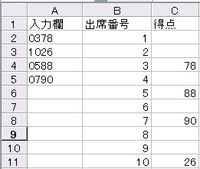
そこでなるべくラクができるように入力欄に出席番号と得点を入力すれば

得点欄に得点が表示されるようなシートを作って欲しいのです。(^O^)

★シートの例

*

*

*

*

*

*

*

*

★仕様

１．生徒数は４５名まで。得点は０～１００までの整数。

２．A列２行目からが入力欄。B列はどう使おうと自由。C列は得点表示欄。

　ただし、2行目が出席番号１の者の得点、3行目が出席番号２の者の得点、・・・・・・となる。

すみません、２の縛りは無しにします。本家のエクセルコンテスト同様

解答用サンプルシートのレイアウトはあくまでも参考ということで・・・

途中で仕様を変えてスミマセンm(__)m

★解答用サンプルシート

2009_Q5.xlsをダウンロード

★くまぷーの解答公開2/11午後8時（答え合わせ）

　直接、解答に関わるような書き込みは2/11午後8時までご遠慮下さい。

　参加して頂ける方は、メールにファイルを添付して送って下さい。m(__)m

minmaxさんのDec2Bin

エクセルには１０進数を２進数に変換するDec2Binという関数が

あります。これはエクセル２００７ならば標準装備なのですが

古いエクセルではアドインの「分析ツール」を組み込まなければ

使えません。ちょっと不便です。それに変換できる１０進数の

上限が５１１までという制限があります。あまり、使い勝手が

よくありません。

　ところが、このブログの常連のminmaxさんが１０進数の１０２３まで

対応する関数を作ってくれました。「関数で解けますか？・・・

ナップサック問題解答例」のコメントの中にその関数があるのですが

このままでは埋もれてしまいそうです。そうなったら、あまりにも

もったいないので改めてここに紹介させて頂きます。

=TEXT(SUM(INT(MOD(十進数,2^ROW($1:$10))/2^(ROW($1:$10)-1))*10^(ROW($1:$10)-1)),"0000000000")

２進数に変換する１０進数を上式の赤文字の十進数のところに

入れて、Ctrl+Alt+Enterを同時に押します。配列数式です。

便利ですよ！！　(^O^)

*************************************************************************

minmaxさんのDec2Binを使って「10枚の領収書」の問題を解いてみました。

すっきりと出来ました。(^O^)

Q4_2009_with_MinMaxSan_DIc2Bin.lzhをダウンロード

関数で解けますか？・・・ナップサック問題解答例

　当初は総当たりの解答しか、用意していなかったんですが

ジョー３さんから、芸がないとのお叱りを受け急遽、別解を

用意しました。三四郎版は当初予定していたものと同じです。

エクセル版は循環参照を利用していますので

他のファイルを開かないで下さい。

三四郎版は圧縮しないと７７４KBですが、エクセル版は１６KBです。

receipt_sanshiro.lzhをダウンロード

Q4_kumapooh_Kaitei.lzhをダウンロード （Excel２００７　改訂版）

Q4_kumapooh_Kaitei_xls.lzhをダウンロード （Excel２０００－２００３改訂版）

※エクセル版はDec2Bin関数を使っています。Excel２００７ならば

そのまま動きますがExcel2000等ではアドイン「分析ツール」を

組み込む必要があります。

　「Excel２０００－２００３」用はエクセル２００７で保存し直しただけで

動作の検証はしていません(^^ゞ

******************************************************

エクセルの改訂版をアップしました。（2009/02/02）

関数で解けますか？

あるSNSで出された問題のパクリなんですが・・・

【問題】
ある電器屋では7777円以上のレシートを持って行くと
景品として、幻のVB for MS-DOSのFDをくれる。
次の10枚のレシートから選んで7777円 に近くなるような
組合せを１つ見つけて欲しい。

　1922　1766　1598　1246　1153　1000　961　869　593　267

ちなみに下のぷーさんが持っているのが
幻のVB for MS-DOSのFDだ！！

＊

＊

*

*

*

*

*

*

*

*

★解答用のエクセル・三四郎のファイルを用意しました。

ダウンロードしてお使い下さい。

Q4_2009.lzhをダウンロード

平仮名を半角カタカナに（エクセル関数編）

　「平仮名を半角カタカナに」というキーワードでここを訪れる方が

かなりいらっしゃるようだ。

その時はVBAのStrConvを使う方法だったのでVBAを使わない

方法を紹介したい。

（例）A1に「くまぷー」とあるとして、B1に「ｸﾏﾌﾟｰ」と表示させる。

手順

１．B1に=PHONETIC(A1)

２．A1を選択して「書式」「ふりがな」「設定」

３．「ふりがなの設定」ダイアログボックスの「ふりがな」タブから

　　「種類」を「半角カタカナ」にして「OK」

三四郎と違ってエクセルには平仮名-カタカナ変換の関数が無いので

けっこうエクセルに詳しい方でもこの辺りをご存じない方もいらっしゃるようだ。

実はこの盲点を狙って出題したのが「ごじらをばらばらに（エクセル編）」でした。(^^ゞ

ごじらの逆襲

（●｀ε´●）：なんだ、みんな、ごじらをばらばらにするのに

　　　　　　　100文字を越えているのか？！おいらなんか

　　　　　　　たったの22文字だよ！！（￣＾￣）

＊

*

*

*

*

【´･ω･`】:べべちゃん、「ゴジラ」のゴジラと「ゴジラの逆襲」の

　　　　　ゴジラは・・・

ごじらをばらばらに・・・エクセル編【解答例】

問題はこちら

さて、この問題のポイントは、濁点・半濁点を親文字から分離するのですから

親文字である平仮名を如何に半角カタカナに変換するかです。

ところが、エクセルには全角半角変換の関数はあるが

平仮名カタカナ変換の関数が用意されていません。VBAを使うなら

Strconvでも使えばいいんですが、ルールでVBAは禁じ手です。

さて・・・そこでどうするかが頭の使いどころです。

minmaxさんの「地球防衛軍」にも対応していますよ、という言葉・・・

それは、タネは全てお見通しですよ、と言う宣言ですね(^^ゞ

だって「地球防衛軍」という漢字が平仮名に変わるんだもん、フリガナ関数（phonetic）を

使っているのはバレバレですよね・・・(^^ゞ

phoneticによるフリガナはデフォルトで全角カタカナになりますので

これを利用します。

手順（基本的な考え）

１．phoneticで平仮名を全角カタカナに

２．Ascで全角カタカナを半角カタカナに

３．midでばらばらにして１文字ずつ切り出す

４．jisで全角カタカナに

５．codeで文字コードを取り出す

６．文字コードから２５６を減じて全角カタカナのコードから

　　全角平仮名のコードに修正

７．charで全角平仮名のコードを文字に

【解答例】

=IFERROR(CHAR(CODE(JIS(MID(ASC(PHONETIC($A2)),COLUMN()-1,1)))-256),MID(ASC(PHONETIC($A2)),COLUMN()-1,1))

（エクセル２００７　１０４文字）

ごじらをばらばらに・・・エクセル編

【´･ω･`】：A1に「ごじら」とあったら

　　　　　　　　　　B1に「こ」

　　　　　　　　　　C1に「゛」

　　　　　　　　　　D1に「し」

　　　　　　　　　　E1に「゛」

　　　　　　　　　　F1に「ら」

　　　　　　・・・といったふうにバラバラに表示させたいんだ。

　　　　　　どうやったらできるかなぁ・・・？　(^。^)

★今回のルール

１．三四郎厳禁　(^^ゞ

２．VBA禁止

３．B1の式をF１までコピペして答えを作る。

関連：「ごじらをばらばらに」（三四郎編）

http://www.geocities.jp/kuma_pooh1958/Blog/sns_Codzilla_Index.html