Excel Maniacs

第53回 十枚の領収書（その２）

　ジョー３さんから「MAB５３」という問題ファイルが送られてきた。

これは例の「ナップサック問題」で「関数で出来ますか～？」の

第４回「十枚の領収書」で既に取り上げたものだと思うのだが・・・

【問題ファイル】

MAB53.xlsをダウンロード

＊

＊

*

*

*

*

第52問 おいらの関数・・・ 問題＆解答例

supermabさんから「関数で出来ますか～？」用に頂いた問題を

倉庫の奥に封印していました。しかし、興味があるので見せてみろと

いう声が高まってきたのでその封印をときます。

それは・・・オイラーのΦ関数です。

**************************************************************************************

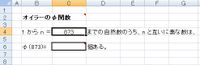
　オイラーのφ関数は、

　正の整数 n に対して、1 から n までの自然数のうち
　n と互いに素なものの個数を φ(n) として与えることによって定まる
　数論的関数 φ である。

　例えば、1, 2, 3, 4, 5, 6 のうち 6 と互いに素なのは 1, 5 の 2 個であるから、
　定義に拠れば φ(6) = 2 である。

　また例えば 1, 2, 3, 4, 5, 6, 7 のうち 7 以外は全て 7 と互いに素だから、φ(7) = 6 と定まる。

　慣例的に φ(n) と表記されるため、オイラーの φ 関数（ファイかんすう、phi function）とも呼ばれる。

　※：上の説明は、「http://ja.wikipedia.org/wiki/オイラーのφ関数」 の引用です。

問題

セルC4に２以上１０００以下の整数を入力し、それをｎとする時、

φ(n)をセルC6に表示させよ。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　（supermabさん談）

*

*

*

*

*

supermabさんの参考ファイル：up0390.zipをダウンロード