最初に作った問題と比べ、可也難易度を和らげることが出来たと思います。
しかしわたしが出題した前回・前々回の問題と比べますと
まだまだその比では無いと思います。
と言うことでヒントにならないヒントを。
←・・・(それってヒント?)
あることに気が付くとその難度は愕然と低下。
もっともそれに気付き難いからこそ、、、高難度なのか。
この問題の意図は条件にあります。
従いまして条件の変更はこの問題の意味無し。
が、、、それはあくまでエクセル学(そんな単語聞いたこと無い)の追求。
故にそんな固いことは言いません。
如何しても出来ない、、、そんな時は、配列・作業列を使ってください。
少ない文字数で、、、の問題ではありません。
文字数はあくまで結果としてください。
(からくちさん談)
【問題】
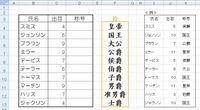
出目(C列)の数値が大きい順にF列の位を称号(D列)に表示する。
≪条件 その1≫
仮に最大値が2名居た場合、その2名共に1番上の『皇帝』の称号を与える。
その次に大きい数値(3番目)には2番目の位である『国王』の称号を与える。
RANK関数の順位の付け方と違い順位を飛ばさない。(1位・1位・3位では無く1位・1位・2位とすること)
≪条件 その2≫
※ 答え(式)はD4に入れその式をD13まで、、、とする。
※ セル参照(C4)は構いませんが、範囲指定は列指定(C:C)のみとする。(C4:C13は禁止)
※ 配列数式の禁止。(INDEX・MMULT等でCtrl + Shift + Enterの代わりをするのも当然禁止)
ただし通常の使用法でのINDEX・MMULT等の関数使用は制限するものではありません。
※ 作業列・名前・書式等の使用も、今までの問題と同様に禁止。
*
*
*
*
*
*
*
解答用参考ファイル:Q36_2009.lzhをダウンロード
***********************************************************************
尚、解答発表は9/25(土)の8:00です。それまでは直接数式を
書き込むこと・ポイントとなる関数名を書き込むことはご遠慮ください。
***********************************************************************
>若し10名では無く50名なら・100名なら・・・
少なくとも私の191は人数とは関係ないです^^
投稿情報: y sakuda | 2009年9 月24日 (木曜日) 午後 08時36分
>100以下が出なかったら、延長1週間でも、いいべーーー
それもありかも^^
投稿情報: y sakuda | 2009年9 月24日 (木曜日) 午後 08時47分
>100以下が出なかったら、延長1週間でも、いいべーーー
それでよければ延長しますけど・・・
投稿情報: くまぷー | 2009年9 月24日 (木曜日) 午後 08時54分
延長しても出るかどうか>100以下
限りなくブラックに近いグレーでは61ってのがありますけど、多分からくちさんに「同じじゃん」て言われるの確実w
投稿情報: y sakuda | 2009年9 月24日 (木曜日) 午後 09時14分
ただいまーーー
>少なくとも私の191は人数とは関係ないです^^
ぎょ・・・&がくっ・・・・・
ん、、、
ふふふ・・・・・
これは、良いこと聞いた。・・・・かも、、、
投稿情報: ジョー3 | 2009年9 月24日 (木曜日) 午後 09時24分
>少なくとも私の191は人数とは関係ないです^^・・・その2
ごめんごめん・・・・
よくかんがえたら、おらのもそうだったーーーー
で、勘違いしたのは
階級の下に、、
農民
商人
奴隷
・・・・
・・・・
なんて、、
20個ぐらい続いたら・・・・・
どひゃーーーではある。・・・・
50このくらいがあったら・・・・・・・
ぞぞーーーーーー、、、
投稿情報: ジョー3 | 2009年9 月24日 (木曜日) 午後 09時37分
またまた、、、ごめん、、、
呑むと書きたくなる。
あのーーーーー
ランク入りですかーー
ってことは、、多くの方が見てる
・・・・・=しつげん:ご覧になっている。
ってことは、、
私は、恥さらしをしてるかもねーーー
ちょっと、、、呑んだら書くな・・・・にしなくっちゃ。・・・・
投稿情報: ジョー3 | 2009年9 月24日 (木曜日) 午後 09時40分
>50このくらいがあったら・・・・・・・
50でも100でもまったく変わらず、同じ式
投稿情報: からくち | 2009年9 月24日 (木曜日) 午後 10時04分
>>50このくらいがあったら・・・・・・・
>50でも100でもまったく変わらず、同じ式
ふふ・・・そうだと思った。(できてねーーけど)
で、、さいころを4っつ転がしたら・・・・
皇帝さんとか
王さんは、、、
なかなか、出なくて、、、遊べそうではある
・・・・・
f9、f9、f9・・・・・・100回ほど・・・・
で、でたーーー皇帝・・・・とか、、、
投稿情報: ジョー3 | 2009年9 月24日 (木曜日) 午後 10時16分
>なかなか、出なくて、、、遊べそうではある
今の設問だと必ず出てくるとオモフ・・・・
大分飲んでるみたいだなw
投稿情報: y sakuda | 2009年9 月24日 (木曜日) 午後 10時28分
延長について。
延長しても良い理由:
む印sさん,minmaxたちがほとんど顔をだしてない>時間があればなにかやってくれそう
#私は多分延長してもだめw
延長したくない理由:
個人的には白旗状態何で、早くからくちさんの模範解答見たいw
投稿情報: y sakuda | 2009年9 月24日 (木曜日) 午後 10時33分
>む印sさん,minmaxたちがほとんど顔をだしてない>時間があればなにかやってくれそう
なるほど・・・
では出題者であるからくちさん
延長に対するご意見は?
投稿情報: くまぷー | 2009年9 月24日 (木曜日) 午後 10時38分
からくちさんから問題を頂きました。
この場を借りてお礼申し上げます。
それとsakudaさんからも頂く予定なので
あと2回は大丈夫かと・・・
投稿情報: くまぷー | 2009年9 月24日 (木曜日) 午後 10時43分
>>なかなか、出なくて、、、遊べそうではある
>今の設問だと必ず出てくるとオモフ・・・・
>大分飲んでるみたいだなw
そそ、、、、
そうかいーーー
ってわけで、、
=INT(RAND()*6)+1+INT(RAND()*6)+1+INT(RAND()*6)+1+INT(RAND()*6)+1
で、、、10段作って・・・・
100回押してみた。
うーーん、、、
sakudaさんは、、、
確率論??も、すごいのねーーー
100回で
24(=皇帝)が、3回も出たのだった)
そおーーかーーー
1回ぐらいと思ったけど、、、
(これは飲んだせいでなく、考えが足りないようだ)
投稿情報: | 2009年9 月24日 (木曜日) 午後 10時48分
「数字を作る その3」を作ろうとした
もの凄く辛い、"100倍"カレー
めちゃくちゃ辛い、"200倍"カレー
、、、て、この差、、、分かるのかな~
「出た目で称号を獲得」より"150倍"難問かも
このままでは、まだまだとても出題出来ない
投稿情報: からくち | 2009年9 月24日 (木曜日) 午後 10時51分
>sakudaさんは、、、
>確率論??も、すごいのねーーー
いや~、最大値が皇帝だから・・・
さいころを振れば必ず最大値は存在するわけで・・・
投稿情報: くまぷー | 2009年9 月24日 (木曜日) 午後 10時51分
>もの凄く辛い、"100倍"カレー
>めちゃくちゃ辛い、"200倍"カレー
痔になりそう・・・
投稿情報: くまぷー | 2009年9 月24日 (木曜日) 午後 10時52分
なんか、、はまりそう・・・・
もう1回
f9・・・・・178回でようやく、、、24(皇帝)だった。。
確率は、、、気まぐれなのだ。
もう1回やってネルーーー。。。
投稿情報: ジョー3 | 2009年9 月24日 (木曜日) 午後 10時56分
さいころ10個なら
合計の目の出やすいのは、、、
35ですよねーーー
まず、、、
60は、、、、でるけど、、、でにくいよねーーー
って、だけです。。
投稿情報: | 2009年9 月24日 (木曜日) 午後 11時02分
>延長に対するご意見は?
う~~ん、、、難しい質問ですね
みなさんが延長してまでこの問題に取組みたい、と考えているか、、、疑問
みなさんがエクセルの面白さをどの方向に、どの距離に感じているか、、、分からない
と言うことで、わたしの見解としては、、、何時もの通りがいいように思います
投稿情報: からくち | 2009年9 月24日 (木曜日) 午後 11時07分
sakudaさんから問題を頂きました。
ありがとうございます。
これで38回までは大丈夫。
からくちさんが続いているので
次回はsakudaさん出題の予定ですm(__)m
投稿情報: くまぷー | 2009年9 月24日 (木曜日) 午後 11時08分
>「出た目で称号を獲得」より"150倍"難問かも
>このままでは、まだまだとても出題出来ない
うーん、、、たまにいいと思います。
世に隠れている・・・・超人が、、、
ではーーーー
って、・・・・・・
・・・・・
出ておいでになるかもしれないから。
・・・・・・・
投稿情報: ジョー3 | 2009年9 月24日 (木曜日) 午後 11時08分
>何時もの通りがいいように思います
わかりました。
出題者さんがそうお考えであるならば
いつもの通りということで行きましょう(^o^)
投稿情報: くまぷー | 2009年9 月24日 (木曜日) 午後 11時09分
>sakudaさんから問題を頂きました。
問題にもならない問題w
面白い解法があるかどうかも分からないという無責任な代物ですwww
投稿情報: y sakuda | 2009年9 月24日 (木曜日) 午後 11時11分
>178回でようやく、、、24(皇帝)だった。。
凄いです
サイコロを4つ振ってオール6が出る確率99%は、、、5964回
178回では可也ラッキーと思います
投稿情報: からくち | 2009年9 月24日 (木曜日) 午後 11時18分
あーーーー
きょうは、、、忙しかった。
でも、、、
蟹をもらって、・・・・・・
これは美味かったーーーー・・・・
投稿情報: jyo-3 | 2009年9 月25日 (金曜日) 午後 08時23分
分からない・・・・
確率論:
6が出る(さいころ)確率=1/6
それが、起こったときに、さらに6が出る・・・
=(1/6)*(1/6)・・・・・ほんと?
だとしたら、
4個のさいころ、、、全部6は??
=(1/6)^4・・・・=0.077% ?
ん、、、6^4??
1296回に1回の割合??
あーーーー
確率論って、、わからん、、
投稿情報: ジョー3 | 2009年9 月25日 (金曜日) 午後 09時27分
きょうは、、、
答えあわせが、遅いですね~ ^^;
投稿情報: supermab | 2009年9 月25日 (金曜日) 午後 09時27分
おいおい・・・よってる?・・・何曜日??
・・・・・・すまん、すまん
投稿情報: じょー3 | 2009年9 月25日 (金曜日) 午後 09時30分
>答えあわせが、遅いですね~ ^^;
待ち構えてる・・・・
なんか秘策があるみたいだな^^
σ(^^)は白旗です
投稿情報: y sakuda | 2009年9 月25日 (金曜日) 午後 09時33分
>なんか秘策があるみたいだな^^
そかそか、、、
悪かった、、、、
1日間違いなんて、思って、御免名、、
投稿情報: ジョー3 | 2009年9 月25日 (金曜日) 午後 09時40分
( ̄□ ̄;)ギョッ
明日も仕事かよ~~~
>待ち構えてる・・・・
ご、、誤解です。。。
ギブアップです~
で、
早く答えが、、、見たくって ^^;;;
で、
たとえば、、、
=SUM({1,2,3})
って、配列数式ですよね~?
などと、
話をそらしてみたり・・・
基本的なことを聞いてみたりして・・・
あはは、、、^^;;;
(照れ隠しにわらってみた)
投稿情報: supermab | 2009年9 月25日 (金曜日) 午後 09時48分
>( ̄□ ̄;)ギョッ
>明日も仕事かよ~~~
・・・ということはここで
今日が金曜日だと気がつかなければ
明日、無断欠勤だったりして・・・
投稿情報: くまぷー | 2009年9 月25日 (金曜日) 午後 10時01分
>=SUM({1,2,3})
>って、配列数式ですよね~?
厳密な定義があるかどうか知りませんが、私の解釈では「配列定数を使っている式」です。
ただし、今回のからくちさんの出題意図は「配列をつかわない」ということのようです。
投稿情報: y sakuda | 2009年9 月25日 (金曜日) 午後 10時06分
>「配列をつかわない」ということのようです。
そーですよね ^^;
一つ一つ、、ちまちま調べても
ヾ(`◇')ダメッ!
って事ですね~
投稿情報: supermab | 2009年9 月25日 (金曜日) 午後 10時19分
>1296回に1回の割合??
1万回でも100%とは言い切れない計算式
>出題意図は「配列をつかわない」ということのようです。
出題者解答と一緒に
この問題の出題意図を簡単に書いておきました
、、、て、もう既にお送り済みですが
「数字を作る その3」が出来ました
1番最初の案では、、、
作業列あり : エクセルと出会って1ヶ月頃のわたしでも出来たと思う
作業列なし : う~~~ん、どう考えたらいいのか・・・
これでは出題出来ない
と言うことで、、、第2案
うん、これ位ならいいかな・・・
でも、送ろうか、、、どうしよう、、、
わたし的には
出題者 : 回答者 = 1 : 9
圧倒的に、、、回答者が好き
投稿情報: からくち | 2009年9 月25日 (金曜日) 午後 10時56分
>圧倒的に、、、回答者が好き
x2
の、3乗くらい!
でも、申し訳ないような気もします ^^;;;
投稿情報: supermab | 2009年9 月26日 (土曜日) 午前 12時25分
>圧倒的に、、、回答者が好き
大体皆さんそうなのでは?
からくちさんは余裕で構えてますが、普通は、あっと言う間に出題者の想定を超えて、出題者自身は何も思い付かないなんて羽目にw
今日、所用があり、長時間電車にのってたので、その間ああでもないこうでもないと考えてましたが結局何もでてこなかった・・・
からくちさんのコメントからすると、SumifとかCountifのように範囲を引数にする普通の関数の組み合わせで種類の個数を数えられるということなんでしょうけど・・・
何を考えても配列使う方向へ行っちゃう^^;
投稿情報: y sakuda | 2009年9 月26日 (土曜日) 午後 06時10分
>種類の個数を数えられる
これは配列数式を組む時の考え方では・・・
また、作業列を使う場合も配列と同様の考え方をすることも、、、
一般式と配列数式では考え方が違っても不思議ではない
と言うか同じ考え方をする必要など無い
つまり、種類数は求めていません
投稿情報: からくち | 2009年9 月26日 (土曜日) 午後 07時26分
こんばんは。
SUBSTITUTE
REPT
RANK
LARGE
などで考えてみましたが、
条件にそう良いアイデアなく
諦めました。
投稿情報: min | 2009年9 月26日 (土曜日) 午後 07時38分
>つまり、種類数は求めていません
うーーん、そうすると最初から方向が間違ってたんだな
激しく手遅れですから、出題者解答を楽しみにしてます^^
投稿情報: y sakuda | 2009年9 月26日 (土曜日) 午後 07時39分